Comment utiliser la calculatrice de probabilité

Qu'est-ce que la probabilité ?

La probabilité est la branche des mathématiques qui étudie la probabilité qu'un événement se produise.  En termes simples, la probabilité répond à la question : « Quelle est la probabilité qu'un événement se produise ? »

Par exemple, lorsque vous lancez une pièce, la probabilité d'obtenir face est de 50 %, tout comme celle d'obtenir pile.  C'est le rapport entre la probabilité d'un événement favorable et le rapport du nombre total d'événements possibles, et c'est sur lui que reposent les éléments fondamentaux de la probabilité.

Types de probabilités

Il existe de nombreux types de probabilités, et chacun permet d'analyser différentes situations :

• Théorique : il s'agit de la probabilité d'un événement basée sur des faits ou une logique.  Par exemple, la probabilité d'obtenir un 3 avec un dé à six faces est de 1 sur 6.
• Expérimental : ce type de probabilité sera déterminé à partir d'une expérience ou de l'observation d'un événement.  Plus le nombre d'expériences réalisées est élevé, meilleure sera l'estimation de la vraisemblance.
• Subjectif : Cela repose sur votre jugement subjectif ou votre croyance en la formation d'une probabilité.  Par exemple, une personne peut subjectivement estimer la probabilité de gagner un billet de loterie en se basant sur sa croyance en sa chance.

À quoi sert le calculateur de probabilités ?

Le calculateur de probabilités permet de calculer très facilement la probabilité de divers événements.  Vous souhaitez peut-être calculer la probabilité de tirer une carte spécifique d'un jeu ou celle d'obtenir un nombre précis en lançant un dé ?  Le calculateur vous permet de trouver la réponse en quelques entrées seulement.

En général, cela fonctionne comme ceci :

• Saisissez le nombre total de résultats possibles : saisissez d'abord le nombre total de résultats possibles.
• Saisissez les résultats souhaités :  Ensuite, saisissez le nombre de résultats favorables ou souhaités.
• Déterminer la probabilité : la calculatrice vous donne la probabilité sous forme de fraction, de format décimal ou de pourcentage.

Comment utiliser le calculateur de probabilités

Il est très facile d'utiliser le calculateur de probabilités ; suivez ces étapes :

Étape 1 : Visitez l'outil.

Étape 2 : Indiquez le nombre de résultats possibles et le nombre d'événements survenus.

Étape 3 : Calculer : cliquez sur le bouton Calculer.

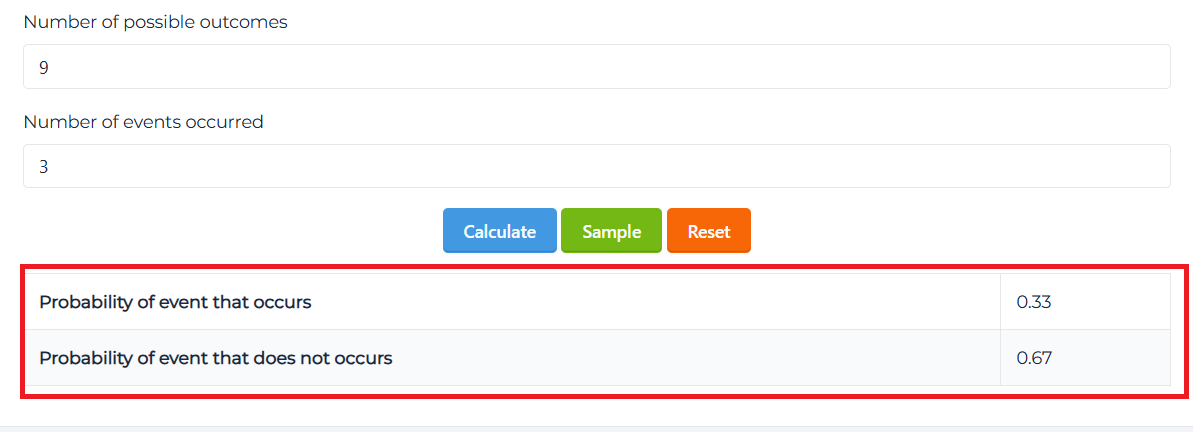
Étape 4 : Afficher le résultat final.

Avantages de l'utilisation d'un calculateur de probabilités

Voici quelques-uns des avantages de l’utilisation d’un calculateur de probabilités :

• Résultats instantanés : la calculatrice vous fournit une réponse instantanée et vous n'avez pas besoin de faire de calculs mentaux compliqués.
• Précision : il fournit des calculs de probabilité précis, sans l'élément humain d'erreur.
• Commodité : il est disponible en ligne, ce qui le rend facile à utiliser chaque fois que vous avez besoin de calculer des probabilités.
• Apprentissage : cela peut être utile aux étudiants et à d'autres personnes qui souhaitent en savoir plus sur les probabilités.

Foire aux questions (FAQ)

1. Quelle est la différence entre la probabilité théorique et la probabilité expérimentale ?

La probabilité théorique repose sur des conditions parfaites, tandis que la probabilité expérimentale repose sur des essais/expériences réels.

2. Comment calculer la probabilité d’événements indépendants ?

Pour les événements indépendants, trouvez les probabilités que chaque événement se produise et multipliez-les ensemble.

3. Puis-je utiliser le calculateur de probabilité pour d’autres événements complexes ?

Oui, le calculateur de probabilité vous permettra de réaliser des opportunités indépendantes, dépendantes et conditionnelles.

4. Quelle est la probabilité de tirer un As dans un jeu de cartes ?

La probabilité de tirer un As dans un jeu de 52 cartes est de 4 sur 52, soit 1/13.

5. Le calculateur de probabilité peut-il fournir des pourcentages ?

Oui, le calculateur de probabilité peut fournir des pourcentages pour vous aider à mieux comprendre la probabilité en termes d'informations quotidiennes.